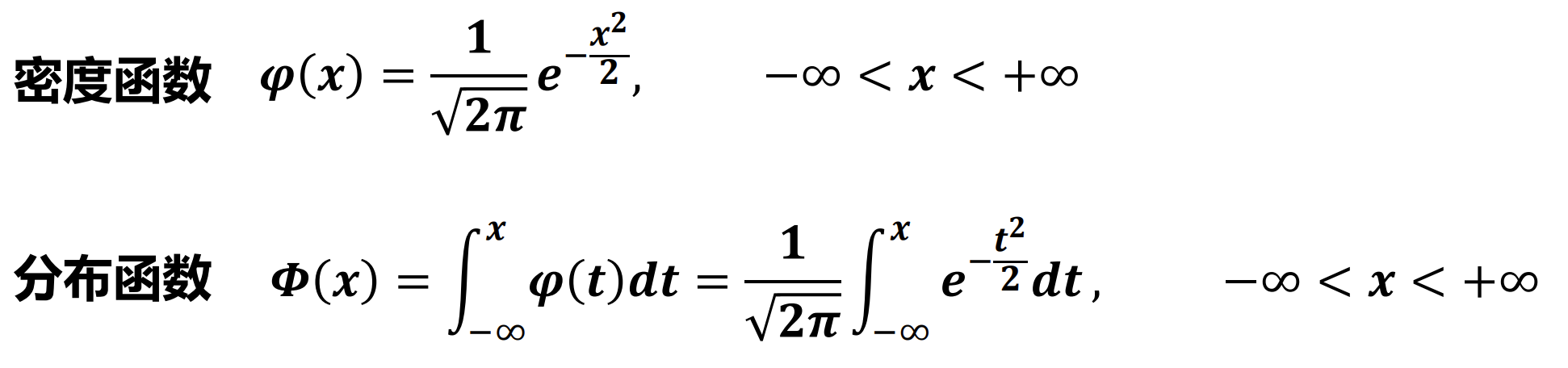1. 连续型随机变量
1.1 定义
设 X 是一随机变量,F(X) 是它的分布函数,若存在一个非负可积函数 f(x), 使得
F(x)=∫−∞xf(t)dt−∞<x<+∞
则称 X 是连续型随机变量,f(x) 是它的概率密度函数,简称为密度函数或概率密度.
- 分布函数连续
- 概率密度函数可以不唯一,允许在有限或者无穷可列个点函数值不同
1.2 几何意义:
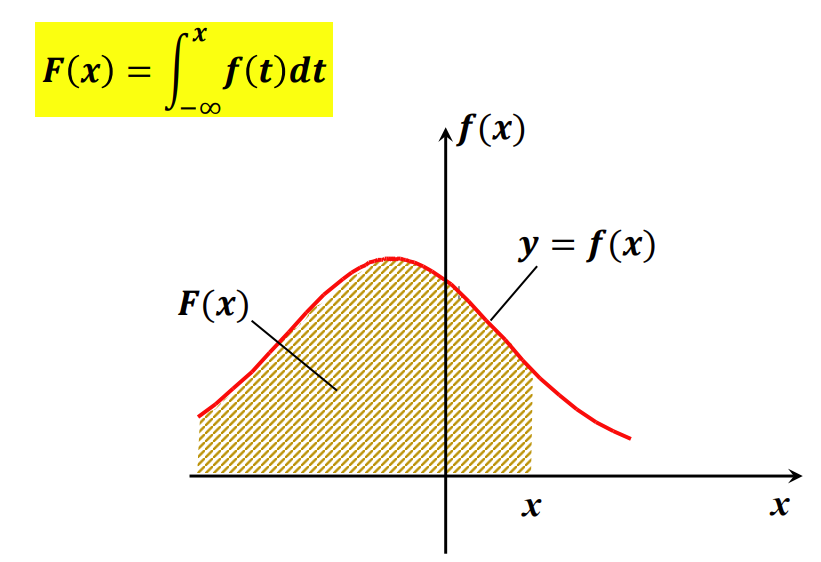
1.3 性质:
- 非负性 f(x)≥0
- 规范性 ∫−∞+∞f(x)dx=F(+∞)=1
- 在 f(x) 的连续点处,F′(x)=f(x),P(x<X<Δx)≈f(x)Δx
- P(x=a)=0
Tips:随机变量并不只有连续型随机变量和离散型随机变量
2. 常见随机变量的分布
2.1 均匀分布
若 X 的密度函数为
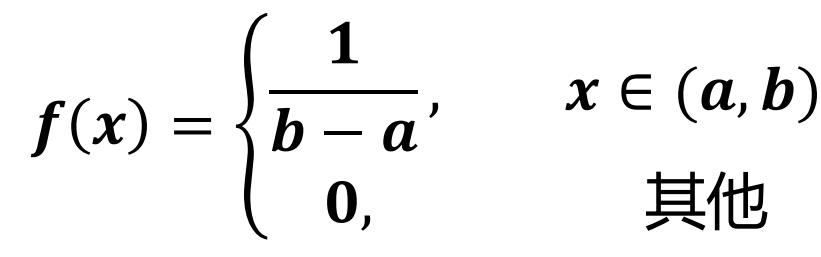
称 X 为 [a,b] 上的均匀分布,记为 X∼U(a,b)
2.2 指数分布
若 X 的密度函数为
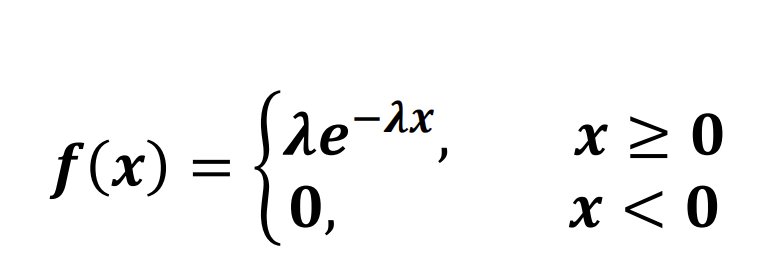 则称 X 服从参数为 λ 的指数分布,记为 X∼E(λ) 或者 X∼Exp(λ)
则称 X 服从参数为 λ 的指数分布,记为 X∼E(λ) 或者 X∼Exp(λ)
性质:
- 无记忆性:P(X>s+t∣X>s)=P(X>t)
- Poisson 分布的联系:若某事件服从 Poisson 分布,则相邻两事件发生之间的时间服从指数分布
2.3 正态分布(Gauss 分布)
若 X 的密度函数为
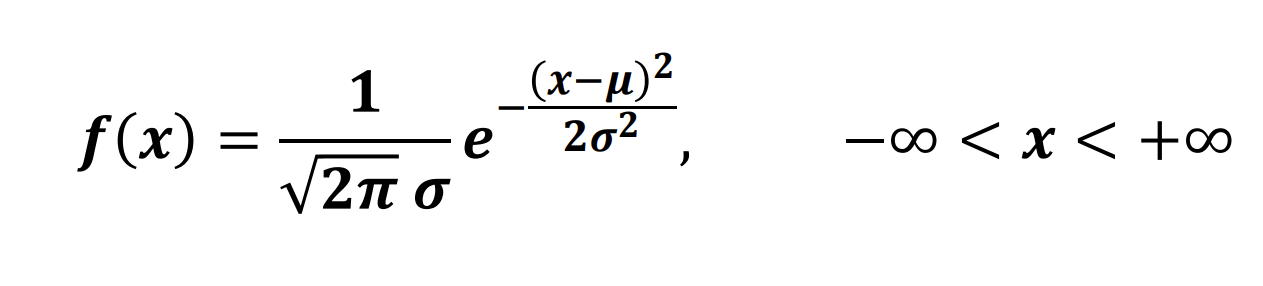 其中 μ 为数学期望,σ2 为方差,则称 X 服从参数为 μ,σ2 的正态分布,记为 X∼N(μ,σ2)
其中 μ 为数学期望,σ2 为方差,则称 X 服从参数为 μ,σ2 的正态分布,记为 X∼N(μ,σ2)
性质:
- 图形关于 x=μ 对称
- 曲线在 x=μ 处有最大值:f(μ)=2πσ1
- 在 x=μ±σ 处有拐点
- 曲线以 x 轴为渐近线
- 图形为单峰状
标准正态分布:
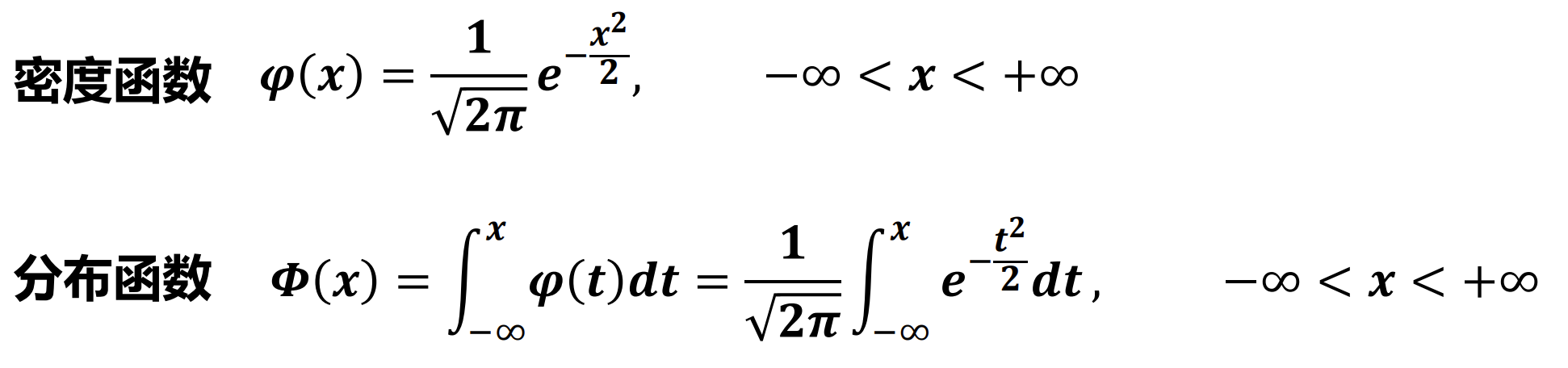
性质:
- Φ(0)=0.5
- Φ(−x)=1−Φ(x)
- P(∣X∣<x)=2Φ(x)−1
一般正态分布化为标准正态分布
设 X∼N(μ,σ2),则 σX−μ=X∗∼N(0,1)

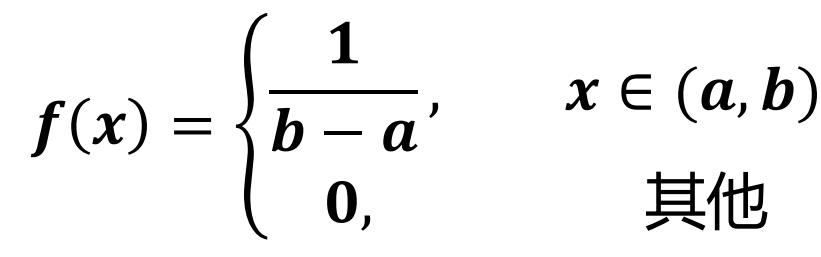
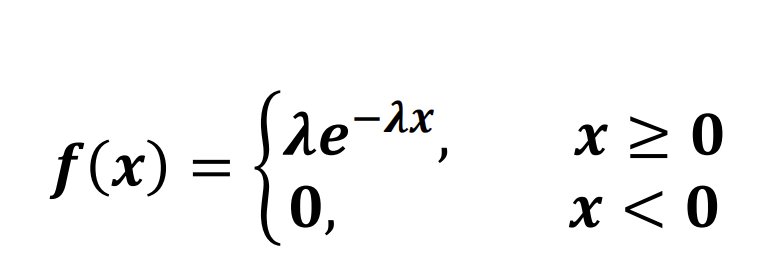 则称 服从参数为 的指数分布,记为 或者
则称 服从参数为 的指数分布,记为 或者 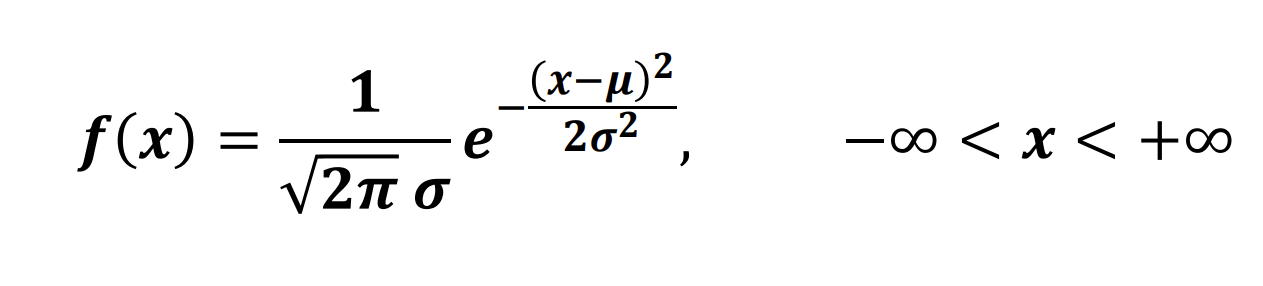 其中 为数学期望, 为方差,则称 服从参数为 的正态分布,记为
其中 为数学期望, 为方差,则称 服从参数为 的正态分布,记为